norswap

aka Nicolas Laurent

Stock Market Adventures: Options & The Wheel

19 Feb 2021

Part of a series on Finance.
Previously: Intro

I said last time I mostly trade using options. In this article I will explain my main strategy, known as the wheel. But first, I'll have to give you a bit of backgrounds on options. I'll finish by a more technical explanation of option pricing and linking to a few other intersting option strategies - in case you're interested.

This is going to be a long post, with a lot of words (and a few numbers). If you'd rather watch videos instead, I strongly recommend Growing Wealth's Options Trading Course. It will teach you option fundamentals, the wheel strategy, and a few others beside. Also no one says you can't read the post and watch the videos ;)

Option Basics

A call option is a contract that allows (but does not force) you to buy 100 shares of a stock at a pre-determined price (the strike price) until some point in the future (the expiration date).

Conversely, a put option allows you to sell 100 shares at a pre-determined strike price until the expiration date.

Actually buying or selling is called "exercising" the option. Options can be American-style — exercisable at any time until expiration, or European-style — exercisable only at expiration. In practice this does not make much of a difference because, excepted in two specific cases, it is always more profitable to sell an option than to exercise it before the expiration date.

(Exceptions explained. Feel free to skip!)

The first exception are that when the stock is going to pay a dividend, the holder of an option may wish to exercise the option to benefit from the dividend.

The second exception is when the option is not very liquid, meaning there is no one interested in buying it at a greater price than the profit you would make by exercising the option. This should be extremely rare, as I expect these market inefficiencies to be arbitraged away.

Options must be purchased for a price which is called the premium. This premium is usually lower than the stock price.

In a simple scenario, if you buy a call option and hold it until expiration, you will profit if the price of the stock ends up being superior to the sum of the strike price and the premium.

call_profit_or_loss = stock_price - (strike_price + premium_paid)

For put options, the logic is reversed, you profit if the stock price goes down enough:

put_profit_or_loss = strike_price - (stock_price + premium_paid)

Try to understand these formulas. The key idea for a call option is that it allows you to purchase the stock at the strike price. If the current stock price is above the strike price, you can buy the stock (through the call option) and sell it for an instant markup.

For a put option, you can sell stock at the strike price. If the stock price is under the strike price, you can buy the stock and sell it (through the put option) for an instant markup.

Who do you buy these options from? Well, anyone really. Anyone that can buy options can also sell options. An option is a contracts formed between two parties, one that "buys" the option, and one that "sells" (or "writes") it.

The person selling the option is making a different bet than the buyer. She is betting that the stock price will not be high enough for a call option to be profitable, or that the stock price will not be low enough for a put option to be profitable.

If that turns out true, the option is said to expire worthless. The buyer does not execute the option (as that would be a money-losing move) and so lost the premium he paid in the trade. The seller, on the other hand, profits by pocketing the premium.

Options are characterized by the triplet [underlying stock, strike price, expiration date], so there a lot of possible combinations.

Three useful abbreviations are used to talk about strike prices: an option can be at the money (ATM) when the strike price is more or less equal to the current stock price, out of the money (OTM) when the strike price is over/under (call/put) the stock price, and in the money (ITM) when the strike price is under/over (call/put) the stock price. When an option expires ITM, you profit, if it expires OTM, you made a loss.

Note that OTM options are not worthless (before expiring) — they represent the potential for the stock price to move in desired direction until the expiration date. It's even possible to make money by trading OTM options that have never been ITM: it suffices to buy an OTM option, and sell it when the stock price has moved in the right direction (up for call, down for put) - so when the option is "less OTM".

Why Use Options

Why use options rather than buy and sell shares? There are multiple reasons.

On the buy side, options offer leverage. We said option premiums are much cheaper than stocks. To give you an idea, let's consider ATM options on Microsoft stock.

Such an option expiring in 20 days currently sells for ~3% of the stock price (in reality, 300% of the stock price, since an option commands 100 shares, but to make things convenient, option prices are usually denominated relative to a single share). For an option expiring in 50 days, the price is ~4.5%. And for January next year, it is ~13%.

That's quite a discount! Of course, it comes at a price. First - there is an expiration. If the option expires worthless, you lose the premium, whereas you can hold stock indefinitely.

Second, your profit margin on the 100 shares commanded by the option is reduced by the premium you paid. It is always more profitable to buy 100 shares than a call, in absolute terms (absolute meaning "if you ignore the amount that you need to invest").

That's where leverage comes in: because options are much cheaper, you can buy more of them compared to the stock - and so if you profit, the profit typically ends up much higher for the same amount of money invested.

The sell side is where, according to me, options really shine.

While buying options (or shares) lets you make money by betting whether the stock will go up or down, selling options lets you make money by betting that the stock price will not fall below a certain price, or rise above a certain price.

To me at least, that's a much easier bet. Stock prices are swingy and hard to predict, but I find it much easier to find conservative bounds for the price movement (especially on the down side).

Even better, this has the magical property of letting you profit after a stock has run up in price. For instance, say a stock flies up from 10$ to 20$. You think it won't go back under 13$, and/or you wouldn't mind owning it as that price (as it is likely to go flying back up at some point in the future). Then you can sell a put with a 13$ strike price expiring in a few feeks. The best thing is, because of the recent price spike, there will be high demand (volatility) for the options and you're likely to sell it a a higher price compared to a similarly-priced, but stable stock. Of course, selling the put when the stock was worth 10$ or 13$ would have been even more profitable, but back then it was much more risky (as its upside was still uncertain).

Finally, selling option lets you do all kind of fancy options combo strategies. I will list a few at the end of the article.

The Wheel

At this point, I'm dying to tell you more about option pricing. Because I'm apparently a finance nerd now, and I find this super cool, but also because it enables very interesting trading strategies.

However, that wasn't quite the premise of this article, which was to describe a fairly conservative strategy using options. I still think you should understand option pricing if you're going to use them, but you don't need to understand all the intricacies to understand the strategy. So here it is.

The strategy is called the wheel. It proceeds as follow:

At this point, I should really give you an example trade. I'm lazy, so I will simply redirect you to the appropriate video from the course I linked earlier.

Let's talk numbers. You should aim for the premium collect when selling the options to be high enough. Jun Hao from the videos I linked before recommends a minimum of 2%. That comes up to a 24% of profit a year, which is fairly reasonable.

Now in pratice, you'll often achieve much better returns than 24%. That's because at some point your covered calls get assigned, you you get the pocket the increase in the stock price. Even for a stock that isn't too volatile, that could be a ~10% increase (it is possible for it be much more, if the stock price increases consistently but never reaches the strike of the calls that you're selling month after month).

What about the downside? Well the downside is the downside of the stock. You can only lose money in this strategy if the stock loses value. That's why picking good stocks is important. There is a lot to be written about stock picking and fundamental analysis, but that won't be in this blog post.

In fact I'm not currently very inclined to write about valuation - I don't feel like I could tell you much more than a few good youtube channels. In fact here are three recommendations:

Back to the downside of the strategy. The downside is strictly less than owning stock. Think about it: not only do you enter at an advantageous point (low price), but you get paid a premium monthly before and after holding. Even in case of loss, you will lose as much as the stock lost, minus all the premium you collected.

The real price of the strategy is missing out on profits. If you really believe in a stock, don't wait until you puts are called, just buy out, or you could miss out. Similarly, if a stock is really poised for growth, selling covered call could amount to selling away most of your profits.

Like I said, this strategy pays on stable stocks where you like the fundamentals and/or the prospects, but where you also don't that the stock is currently selling at a bargain.

Honestly, What I've Been Doing

So the wheel strategy is sort of my base plan. However, in practice, I've deviated from it significantly.

In particular, I mostly sell puts, and I rarely get assigned. And second, I mostly sell puts on relatively hyped stocks, and consequently collect more premium.

This seems relatively contradictory, but in fact isn't necessarily. Because the stocks are popular, they have high volatility, meaning the premiums are higher. Because of that, I can afford to pick a lower strike price (hence also a lower premium) and still make a respectable profit.

Now, it must be said that the market right now is an euphoric bull market. I would be foolish, I feel, to assume that this will last forever.

Another difference from the wheel strategy is that my puts are not all cash-secured (this is only possible if you trade on margin). Since my puts mostly don't get called, this is fine.

However, I must be wary of a particular risk: if the market turns and goes into a downtrend, I could potential be facing assignment on many/most of my puts, which would "blow my account" (since this is more money than I have because the puts are not cash-secured). I'm actively monitoring for such a risk - it can be avoided by buying back the puts while there is still time (which isn't necessarily easy to do — trading psychology is fascinating and would probably deserve a blog post, a book review, or both).

I've also been relatively bummed by my experiences with selling cash-covered calls. There were a few stocks I really liked, that I acquired by selling puts very close to the money (I didn't mind getting called since I liked the stock). I wanted to follow the strategy and sold the puts, but ultimately I would have done better to just let them ride - I was cut out of a major part of the gains that the stocks made immediately after I was assigned.

Another experience was a much more stable stock, where I felt like the amount of premium collected didn't justify the risk taken by the stock going down (and it was going down).

Interestingly, this is also due to the market being so hyper recently. If things tend to go up, selling covered calls is probably not the best move. I expect this leg of the strategy will make more sense in boring times.

Option Pricing

I think a key thing to be able to trade effectively with options is to understand what influences the price of options (the premium).

It's very important to understand that the price of the options, just like the price of the underlying stock, is set by the market. i.e. the price is what someone is willing to pay for it.

In reality, though this is not super important here, there are two components to the price: the bid (what someone is willing to pay) and the ask (what someone is willing to sell for). When the two component meet, an option is sold. The different between the bid and the ask is called "the spread". In a liquid market with a lot of transaction volume, the spread is small. In an illiquid market where not much is happening, the spread is wide.

However, the price of options is influenced by four key factors:

In fact, the price of options can be modelled using these factors, plus a fourth one (volatility). The most popular model is the Black-Scholes model.

Volatility

Volatility is the last factor that helps to fit the model to the market price. You can think of volatility as "demand": when volatility is high there is a lot of trading activity, hence demand for options, meaning the premium rises.

Volatility is typically correlated with sudden changes or swings in the underlyings stock price.

Because volatility helps the model fit to reality, it is called implied volatility, or IV for short. External conditions influence the demand for options, which is reflected in the price, and then we use the Black-Scholes model to extract a quantified measure of "volatility" from the price.

Each stock has its own implied volatility. What qualifies as "high" IV varies from stock to stock. Some stocks are inherently more stable than other. Volatility can also be measured at the level of the market — this is notably done through the VIX index.

It's also theoretically possible to have a stock that has high IV without exhibiting erratic price movements in the underlying stock.

Implied volatility is expressed in percentage. This percentage represents the predicted standard deviation range for the price of the underlying in the next year. So a 100$ stock with an IV of 25% is expected to end within the 75-125$ price range after a year, with 68% probability (one standard deviation).

How does the implied volatility predicts the expected price? Essentially, the higher market participants are willing to bid on an option, the higher the expected price movement — traders are willing to pay more because they expect a big move.

An open question (that I can't answer): why is the range traditionally centered on the current stock price? This is obviously wrong for many stocks.

The Risk-Free Rate

Okay, before we dive in the really important stuff, let's evacuate something that is (currently) not very important: the risk-free rate.

The risk-free rate represents the rate of return of a risk-free investment. It's typically embodied by the yield of US treasury bonds — which can't default unless the US government defaults, at which point we'd all have other worries than the marginal return rates of our options.

It's mostly a non-factor because this rate is at the moment relatively stable, and relatively low. The American federal reserved has vowed to keep this rate low for at least the next two years. I'm a bit in over my head here, but from what I understand, it is widely considered that letting the interest rate increase would do bad things to do economy, and nobody seems particularly eager to do it.

The idea of the risk-free rate as a factor in option price is simple: when the risk-free rate of return increase, you will demande increased returns for the risk that you actually take — which in this case takes the form of decreased premiums. It's also interesting to note that since the option seller pockets the premium up front (and not at expiration), an increased risk-free rate implies a greater ability for him to compound the premium until expiration.

Option Greeks

The most commonly used tool to analyze option prices are the option greeks. The option greeks represent the variation of the option price relative to the factor we listed before (so they are derivatives).

Here are the first-order greeks:

A key considerations when dealing with greeks is that they all represent a rate of change relative to a given variable (price, time, volatility, risk-free rate) when all else stays equal. Said otherwise, the value of every greek depends on every variable. This is why not every option with 30 days until expiration has the same theta - of course the option price for a 10$ stock isn't going to drop as much over time as the option price for a 1000$ stock! The same goes for every other variable. Let us now go over some of these interesting correlations.

Let's start with delta. Delta is about 0.5 when the option is at the money. The more the option gets in the money, the more delta increases, and the more it gets out of the money, the more it decreases.

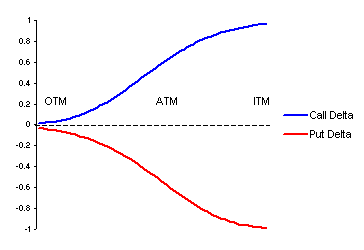
Why? If you own a 10$ call on a 1000$ stock, there is almost no option-specific risk involved in holding the option, so every extra dollar in the underlying price will translate to extra dollar in the option price.

In fact, we can show that the price of an ITM call option must exceed stock_price - strike_price. It that weren't the case, you could exercise the option and immediately make a profit by selling the shares (in reality you would need for the settlement of the shares after exercising the option). A similar logic applies for put option, where the intrinsic value is strike_price - stock_price instead.

The price of options can be divided into two parts. First, the intrinsic value, which is the aforementiond stock_price - strike_price factor (or vice-versa for puts). This factor is capped at 0, however: ATM and OTM shares have a 0 intrinsic value, not a negative one. Second, the time value which represents the potential for the option to appreciate and potentially get in the money (or further in the money).

For call options, the intrinsic value is maximal at the 0 strike price, a point where the time value is also minimal. For puts, it's a bit more complicated, but if far enough strikes are available (*), you will also find put options where the option price is roughly equal to the intrinsic value.

(*) The exchange decides how far the available strikes go, as well as the increment between two available strike prices!

The time value is maximal at the money, and decreases the further out in the money or at the money the option goes. We said the time value represent the potential for appreciation of the option. It does make sense that an option far out of the money is unlikely to ever go into the money, while an option far in the money will more or less move in lockstep with the underlying stock.

Let's tackle this from another angle. Buying a deeply ITM option is like holding stock: there is not much more risk than holding the stock. For this reason, the time value is small — the price of the option will move in lockstep with the underlying. But because the option is far in the money, the intrinsic value is large, and the option is pricey compared to an ATM option.

Buying a deeply OTM option, on the other hand, is more like buying a lottery ticket. It's very likely it will expire worthless. Even if the underlying moves in the right direction and you sell before expiration, the price increase will be small because the further OTM an option is, the smaller delta is. This is therefore mostly a bet on an explosive change in the underlying price. For such a bet to make sense, the option price has to be very low. The intrinsic value is zero, and the time value is low, since the bet is very unlikely to succeed.

Somewhere in the middle, ATM options have 0 intrinsic value, but maximal time value. That's because they are the most swingy of options. Since delta is also maximal (0.5) at the money, the price of ATM options will respond the fastest to changes in the price of the underlying. If your option is ATM a few days before expiration, even a 3% price move is often the difference between a 100% loss and 100% profit at expiration. This potential for a quick profit is what makes the time value high at the money.

Finally, we should mention that, just like time value, theta (the time decay) is greatest at the money. This is because an option has 0 time value at expiration, so the time value must tend to zero over time. When there is more time value (because the option is ATM), it therefore has to decrease faster over time.

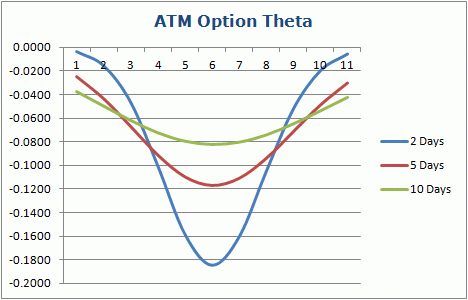
Theta vs Price

In the chart above, the options are ATM and the underlying price is 6. Notice how the curve flattens when the remaining time diminishes — because the time value does too.

As we mentionned somewhere above, the time values decays increasingly fast as expiration nears, and so does theta accelarate:

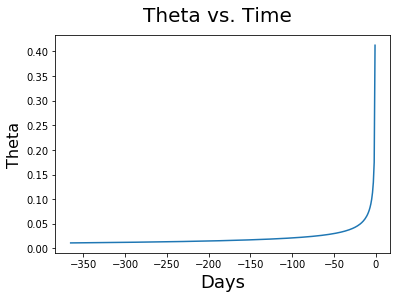
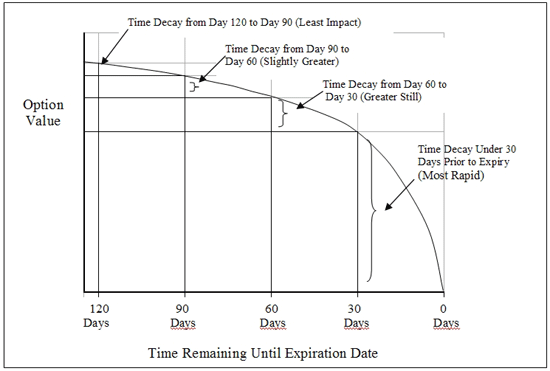
Time Value vs Time

In the chart above "option value" should really be "time value". The option may still have intrinsic value at expiration.

In passing, note that delta also varies with time. At expiration, ITM options (no matter how far) have a delta of 1 (intrinsic value == price), while OTM options have a delta of 0.

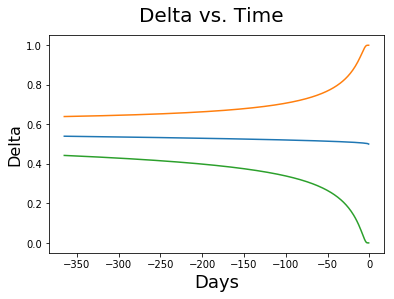
Sources for the charts: 1, 2, 3

And with this, I conclude my rather long exposition on options pricing. The topic is even broader than this. For instance, we didn't talk about the second-order greek gamma (Γ) which played a major role in the recent GameStop rally.

I hope this article has been useful. See you next time!

PS: Some Simple Option Strategies